Теплоизолирующая способность воздушных прослоек
Зазоры, доступные потокам воздуха, являются продухами, ухудшающими теплоизоляционные характеристики стен. Зазоры же замкнутые (так же как закрытые поры вспененного материала) являются теплоизолирующими элементами. Ветронепродуваемые пустоты широко применяются в строительстве для снижения теплопотерь через ограждающие конструкции (щели в кирпичах и блоках, каналы в бетонных панелях, зазоры в стеклопакетах и т. п.). Пустоты в виде непродуваемых воздушных прослоек используются и в стенах бань, в том числе каркасных. Эти пустоты зачастую являются основными элементами теплозащиты. В частности, именно наличие пустот с горячей стороны стены позволяет использовать легкоплавкие пенопласты (пенополистирол и пенополиэтилен) в глубинных зонах стен высокотемпературных бань.
В то же время пустоты в стенах являются самыми коварными элементами. Стоит в малейшей степени нарушить ветроизоляцию, и вся система пустот может стать единым продуваемым выхолаживающим продухом, выключающим из системы теплоизоляции стен все внешние теплоизоляционные слои. Поэтому пустоты стараются делать небольшими по размеру и гарантированно изолируют друг от друга.
Использовать понятие теплопроводности воздуха (а тем более использовать ультранизкое значение коэффициента теплопроводности неподвижного воздуха 0,024 Вт/м град) для оценки процессов теплопередачи через реальный воздух невозможно, поскольку воздух в крупных пустотах является крайне подвижной субстанцией. Поэтому на практике для теплотехнических расчётов процессов передачи тепла даже через условно «неподвижный» воздух применяют эмпирические (опытные, экспериментальные) соотношения. Чаще всего (в простейших случаях) в теории теплопередачи считается, что тепловой поток из воздуха на поверхность тела в воздухе равен Q = α∆Т, где α — эмпирический коэффициент теплопередачи «неподвижного» воздуха, ∆Т — разность температур поверхности тела и воздуха. В обычных условиях жилых помещений коэффициент теплопередачи равен ориентировочно α = 10 Вт/м² град. Именно этой цифры мы будем придерживаться при оценочных расчётах прогрева стен и тела человека в бане. При помощи потоков воздуха со скоростью V (м/сек), тепловой поток увеличивается на величину конвективной составляющей Q=βV∆T, где β примерно равен 6 Вт•сек/м³•град. Все величины зависят от пространственной ориентации и шероховатости поверхности. Так, по действующим нормам СНиП 23-02-2003 коэффициент теплопередачи от воздуха к внутренним поверхностям ограждающих конструкций принимается равным 8,7 Вт/м² град для стен и гладких потолков со слабо выступающими рёбрами (при отношении высоты рёбер «h» к расстоянию «а» между гранями соседних рёбер h/a < 0,3); 7,6 Вт/м² град для потолков с сильно выступающими рёбрами (при отношении h/a > 0,3); 8,0 Вт/м² град для окон и 9,9 Вт/м² град для зенитных фонарей. Финские специалисты принимают коэффициент теплопередачи в «неподвижном» воздухе сухих саун равным 8 Вт/м² град (что в пределах ошибок измерений совпадает с принимаемым нами значением) и 23 Вт/м² град при наличии потоков воздуха со скоростью в среднем 2 м/сек.
Столь малое значение коэффициента теплопередачи в условно «неподвижном» воздухе α = 10 Вт/м² град соответствует понятию воздуха как теплоизолятора и объясняет необходимость использования высоких температур в саунах для быстрого согрева тела человека. Применительно же к стенам это означает, что при характерных теплопотерях через стены бани (50- 200) Вт/м² разница температур воздуха в бане и температур внутренних поверхностей стен бани может достигать (5-20)°С. Это очень большая величина, часто никак и никем не учитывающаяся. Наличие в бане сильной конвекции воздуха позволяет снизить перепад температуры вдвое. Отметим, что столь высокие перепады температур, характерные для бань, недопустимы в жилых помещениях. Так, нормируемый в СНиП 23-02-2003 температурный перепад между воздухом и стенами не должен превышать 4°С в жилых помещениях, 4,5°С в общественных и 12°С в производственных. Более высокие перепады температур в жилых помещениях неминуемо приводят к ощущениям холода от стен и выпадению росы на стенах.
 |
|
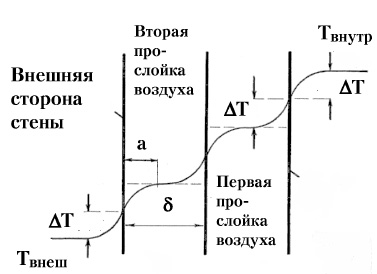
| Рис. 35. Распределение температуры в стене, состоящей из замкнутых (несообщающихся) воздушных прослоек, образованных тремя стальными (или стеклянными) пластинами (в предположении полного отсутствия лучистых тепловых потоков). Поток тепла справа налево. Температура внутреннего воздуха Твнутр выше температуры внешнего воздуха Твнешн. На каждой поверхности образуется пограничный теплопередающий слой толщиной а = (1-3) см с перепадом температуры ∆T. Поток тепла равен Q = ∆T/R = (Твнутр — Tвнешн)/6R, где R = 0,1 м² град/Вт — термическое сопротивление пограничного слоя, не зависящее от толщины воздушных прослоек δ, если а < δ. |
Используя введенное понятие коэффициента теплопередачи от поверхности в воздух, пустоты внутри стены можно рассматривать как последовательное расположение теплопередающих поверхностей (см. рис. 35). Пристеночные зоны воздуха, где и наблюдаются вышеуказанные перепады температур ∆T, называются пограничными слоями. Если в стене (или стеклопакете) имеются два пустотных промежутка (например, три стекла), то фактически имеется 6 пограничных слоев. Если через такую стену (или стеклопакет) проходит тепловой поток 100 Вт/м², то на каждом пограничном слое температура изменяется на ∆T = 10°С, а на всех шести слоях перепад температуры составляет 60°С. Учитывая, что тепловые потоки через каждый в отдельности пограничный слой и через всю стену в целом равны между собой и составляют всё же 100 Вт/м², то результирующий коэффициент теплопередачи для стены без пустот («стеклопакет» с одним стеклом) составит 5 Вт/м² град, для стены с одной пустотной прослойкой (стеклопакет с двумя стёклами) 2,5 Вт/м² град, а с двумя пустотными прослойками (стеклопакет с тремя стёклами) 1,67 Вт/м² град. То есть, чем больше пустот (или чем больше стёкол), тем теплей стена. При этом теплопроводность самого материала стен (стёкол) в этом расчёте предполагалась бесконечно большой. Иными словами, даже из очень «холодного» материала (например, стали) можно в принципе изготовить очень тёплую стену, предусмотрев лишь наличие в стене множества воздушных прослоек. Собственно, на этом принципе и работают все стеклянные окна.
Для упрощения оценочных расчётов удобней использовать не коэффициент теплопередачи α, а его обратную величину — сопротивление теплопередаче (термическое сопротивление пограничного слоя) R = 1/ α. Термическое сопротивление двух пограничных слоев, отвечающее одному слою материала стены (одного стекла) или одному воздушному промежутку (прослойке), равно R = 0,2 м² град/Вт, а трёх слоев материала стены (как на рисунке 35) — сумме сопротивлений шести пограничных слоев, то есть 0,6 м² град/Вт. Из определения понятия сопротивления теплопередаче Q =∆T/R следует, что при том же тепловом потоке 100 Вт/м² и термическом сопротивлении 0,6 м² град/Вт перепад температуры на стене с двумя воздушными прослойками составит те же 60°С. Если же число воздушных прослоек увеличить до девяти, то перепад температуры на стене при том же тепловом потоке 100 Вт/м² составит 200°С, то есть расчётная температура внутренней поверхности стены в бане при тепловом потоке 100 Вт/м² повысится с 60 °С до 200°С (если на улице 0°С).
Коэффициент теплопередачи является результирующим показателем, комплексно суммирующим последствия всех физических процессов, происходящих в воздухе у поверхности теплоотдающего или тепловоспринимающего тела. При малых перепадах температур (и малых тепловых потоках) конвективные потоки воздуха малы, теплопередача в основном происходит кондуктивно за счёт теплопроводности неподвижного воздуха. Толщина пограничного слоя составляла бы малую величину, всего лишь a=λR=0,0024 м, где λ=0,024 Вт/м град — коэффициент теплопроводности неподвижного воздуха, R=0,1 м²град/Вт —термическое сопротивление пограничного слоя. В пределах пограничного слоя воздух имеет разные температуры, вследствие чего за счёт гравитационных сил воздух у горячей вертикальной поверхности начинает всплывать (а у холодной — погружаться), набирая скорость, и турбулизируется (взвихривается). За счёт вихрей теплопередача воздуха увеличивается. Если вклад этой конвективной составляющей формально ввести в значение коэффициента теплопроводности λ, то увеличение этого коэффициента теплопроводности будет отвечать формальному увеличению толщины пограничного слоя a=λR (как мы увидим ниже, примерно в 5-10 раз с 0,24 см до 1-3 см). Ясно, что это формально увеличенная толщина пограничного слоя корреспондируется с размерами воздушных потоков и вихрей. Не углубляясь в тонкости структуры пограничного слоя, отметим, что значительно большее значение имеет понимание того, что передающееся в воздух тепло может «улететь» вверх с конвективным потоком, так и не достигнув следующей пластины многослойной стены или следующего стекла стеклопакета. Это отвечает случаю калориферного нагрева воздуха, который будет рассмотрен ниже при анализе экранированных металлических печей. Здесь же мы рассматриваем случай, когда воздушные потоки в прослойке имеют ограниченную высоту, например, в 5-20 раз превышающую толщину прослойки δ. При этом в воздушных прослойках возникают циркуляционные потоки, которые фактически участвуют в переносе тепла совместно с кондуктивными потоками тепла.
При малых толщинах воздушных прослоек встречные потоки воздуха у противоположных стенок зазора начинают влиять друг на друга (перемешиваются). Иными словами, толщина воздушной прослойки становится меньше двух невозмущенных пограничных слоев, вследствие чего коэффициент теплопередачи увеличивается, а сопротивление теплопередачи соответственно уменьшается. Кроме того, при повышенных температурах стенок воздушных прослоек начинают играть роль процессы теплопередачи излучением. Уточнённые данные в соответствии с официальными рекомендациями СНиП П-3-79* приводятся в таблице 7, откуда видно, что толщина невозмущенных пограничных слоев составляет 1-3 см, но существенное изменение теплопередачи наступает лишь при толщинах воздушных прослоек менее 1 см. Это означает, в частности, что воздушные промежутки между стёклами в стеклопакете не следует делать толщиной менее 1 см.
Таблица 7. Термическое сопротивление замкнутой воздушной прослойки, м² град/Вт
| Толщина воздушной прослойки, см | для горизонтальной прослойки при потоке тепла снизу вверх или для вертикальной прослойки | для горизонтальной прослойки при потоке тепла сверху вниз | ||
| при температуре воздуха в прослойке | ||||
| положительной | отрицательной | положительной | отрицательной | |
| 1 | 0,13 | 0,15 | 0,14 | 0,15 |
| 2 | 0,14 | 0,15 | 0,15 | 0,19 |
| 3 | 0,14 | 0,16 | 0,16 | 0,21 |
| 5 | 0,14 | 0,17 | 0,17 | 0,22 |
| 10 | 0,15 | 0,18 | 0,18 | 0,23 |
| 15 | 0,15 | 0,18 | 0,19 | 0,24 |
| 20-30 | 0,15 | 0,19 | 0,19 | 0,24 |
Из таблицы 7 видно, что официальные рекомендации отличаются от введённой нами оценочной величины термического сопротивления воздушного зазора R = 0,2 м² град/Вт не более, чем на 20-25%.
Их таблицы 7 также следует, что более тёплые воздушные прослойки имеют более низкие термические сопротивления (лучше пропускают через себя тепло). Это объясняется влиянием на теплоперенос лучистого механизма, который мы рассмотрим в следующем разделе. Отметим при этом, что вязкость воздуха растёт с температурой, так что тёплый воздух турбулизуется хуже.
 |
|
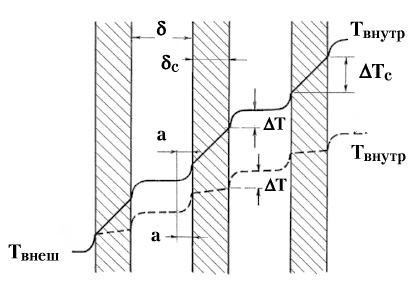
| Рис. 36. Распределение температуры в стене, состоящей из замкнутых (несообщающихся) воздушных прослоек, образованных тремя стенками из низкотеплопроводного («тёплого») материала (в предположении полного отсутствия лучистых тепловых потоков). Обозначения те же, что и на рисунке 35. За счёт низкой теплопроводности материала стенок возникают перепады температур ∆Тc = QRc, где Rc — термическое сопротивление стенки Rc = δc / λc (δc — толщина стенки, λc — коэффициент теплопроводности материала стенки). При увеличении с перепады температур ∆Тc уменьшаются, но перепады температур на пограничных слоях ∆Т сохраняются неизменными. Это иллюстрируется распределением Твнутр, относящимся к случаю более высокой теплопроводности материала стенок. Тепловой поток через всю стену Q = ∆T/R = ∆Тc/Rc = (Твнутр — Tвнешн)/(3Rc+6R). Термическое сопротивление пограничных слоев R и их толщина а не зависят от теплопроводности материала стенок λc и их термического сопротивления Rc. | |
 |
|
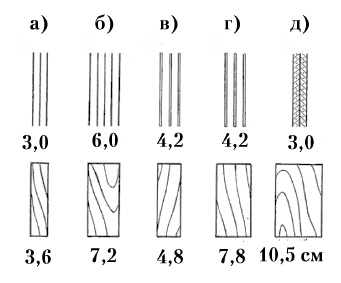
| Рис. 37. Сопоставление теплоизолирующих способностей разных конструкций стен (с учётом внешних пограничных слоев и в предположении полного отсутствия лучистых тепловых потоков, то есть при зеркальных поверхностях): а — три слоя металла (или стекла), отстоящих друг от друга с зазорами по 1,5 см, эквивалентны древесине (деревянной доске) толщиной 3,6 см; б — пять слоев металла с зазорами по 1,5 см, эквивалентны древесине толщиной 7,2 см; в — три слоя фанеры толщиной по 4 мм с зазорами по 1,5 см, эквивалентны древесине толщиной 4,8 см; г — три слоя пенополиэтилена толщиной по 4 мм с зазорами по 1,5 см, эквивалентны древесине толщиной 7,8 см; д — три слоя металла с зазорами по 1,5 см, заполненными эффективным утеплителем (пенополистиролом, пенополиэтиленом или минватой), эквивалентны древесине толщиной 10,5 см. Принятая величина зазоров является условной, эквивалентные толщины древесины в примерах а-г слабо изменяются при изменении величины зазоров в пределах (1-30) см. |
Если конструкционный материал стены обладает низкой теплопроводностью, то при расчётах необходимо учитывать его вклад в теплосопротивление стены (рис. 36). Хотя вклад пустот, как правило, является значительным, заполнение всех пустот эффективным утеплителем позволяет (за счёт полной остановки движения воздуха) существенно (в 3-10 раз) повысить тепловое сопротивление стены (рис. 37).
Сама по себе возможность получения вполне пригодных для бань (по крайней мере, летних) тёплых стен из нескольких слоев «холодного» металла, конечно же, интересна и используется, например, финнами для противопожарной защиты стен в саунах около печи. На практике, однако, такое решение оказывается весьма сложным ввиду необходимости механической фиксации параллельных слоев металла многочисленными перемычками, которые играют роль нежелательных «мостиков» холода. Так или иначе, даже один слой металла или ткани «греет», если не продувается ветром. На этом явлении основаны палатки, юрты, чумы, которые, как известно, до сих пор используются (и использовались веками) в качестве бань в кочевых условиях. Так, один слой ткани (всё равно какой, лишь бы непродуваемой) лишь в два раза «холодней» кирпичной стены толщиной 6 см, а прогревается в сотни раз быстрее. Тем не менее, ткань палатки остаётся намного холодней воздуха в палатке, что не позволяет реализовать сколько бы то ни было длительных паровых режимов. К тому же, любые (даже мелкие) порывы ткани сразу же приводят к мощным конвективным теплопотерям.
Наибольшее значение в бане (так же как и в жилых зданиях) имеют воздушные прослойки в окнах. При этом приведённое сопротивление теплопередаче окон измеряется и рассчитывается на всю площадь оконного проёма, то есть не только на стеклянную часть, но и на переплёт (деревянный, стальной, алюминиевый, пластиковый), который, как правило, имеет лучшие теплоизолирующие характеристики, чем стекло. Для ориентировки приведём нормативные значения термического сопротивления окон разных типов по СНиП П-3-79* и сотовых материалов с учётом теплового сопротивления внешних пограничных слоев внутри и вне помещения (см. таблицу 8).
Таблица 8. Приведенное сопротивление теплопередаче окон и оконных материалов
| Тип конструкции | Сопротивление теплопередаче, м² град/Вт | |
| Одинарное остекление | 0,16 | |
| Двойное остекление в спаренных переплётах | 0,40 | |
| Двойное остекление в раздельных переплётах | 0,44 | |
| Тройное остекление в раздельно-спаренных переплётах | 0,55 | |
| Четырёхслойное остекление в двух спаренных переплётах | 0,80 | |
| Стеклопакет с межстекольным расстоянием 12 мм: | однокамерный | 0,38 |
| двухкамерный | 0,54 | |
| Блоки стеклянные пустотные (с шириной швов 6 мм) размером: | 194x194x98 мм | 0,31 |
| 244x244x98 мм | 0,33 | |
| Поликарбонат сотовый «Акууег» толщиной: | двухслойный 4 мм | 0,26 |
| двухслойный 6 мм | 0,28 | |
| двухслойный 8 мм | 0,30 | |
| двухслойный 10 мм | 0,32 | |
| трёхслойный 16 мм | 0,43 | |
| многоперегородчатый 16 мм | 0,50 | |
| многоперегородчатый 25 мм | 0,59 | |
| Полипропилен сотовый «Акувопс!» толщиной: | двухслойный 3,5 мм | 0,21 |
| двухслойный 5 мм | 0,23 | |
| двухслойный 10 мм | 0,30 | |
| Брусовая стена (для сравнения) толщиной: | 5 см | 0,55 |
| 10 см | 0,91 | |
Источник: health.totalarch.com. Дачные бани и печи. Принципы конструирования. Хошев Ю.М. 2008


Добавить комментарий